格子暗号

格子暗号 (あるいは格子ベース暗号) とは、方式自体あるいは安全性証明において格子を用いる暗号プリミティブを示す一般的用語である。

格子ベースの暗号方式 (公開鍵暗号方式や鍵共有方式) は現在、耐量子暗号の重要な候補となっている。従来広く利用されている公開鍵方式である RSAや 楕円曲線暗号、ディフィー・ヘルマン鍵共有は、量子コンピュータ上で実行できるショアのアルゴリズムによって破られるが、いくつかの格子暗号は古典コンピュータと量子コンピュータの両方に対して攻撃耐性があると考えられている。さらに、多くの格子ベースの方式は、良く研究されている何らかの格子問題 (格子に関連した問題) が効率的に解けないという計算量的な仮定のもとで、安全であると考えられている。

歴史

1996年にミクロス・Ajtaiは、良く知られた格子問題の困難性を利用した最初の格子暗号の構成を示した。 シンシア・ドワークは、短整数解問題 (SIS) と呼ばれる格子問題の平均時の計算困難性が、ある格子問題の最悪時の計算困難性と同等かそれ以上であることを示した。そして、SIS問題の計算困難性と等価な安全性を持つハッシュ関数を示した。

1998年に、Jeffrey Hoffstein、Jill Pipher、Joseph H. Silvermanの3人は、NTRU暗号と呼ばれる格子ベースの公開鍵暗号方式を提案した。 しかし、彼らの方式は、最悪時の格子問題を解くことと等価 (あるいはそれ以上) な安全性を持つかどうかは知られていない。最悪時の計算量的困難性の仮定の下で安全性が証明された最初の方式は、2005年にOded Regevによって提案されている。この論文では、計算困難な問題としてLWE問題 (Learning with Errors問題) も提案されている。それ以降、多くの後続研究がRegevの安全性証明を改善したり 、方式の効率を改善している 。 さらに多くの研究が、LWE問題や関連した問題を元にして、暗号プリミティブを構築することに専念してきた。例えば、2009年にGentryは初めての 完全準同型暗号方式を提案したが、これは格子問題に基づいている。提案されたこの暗号方式では、暗号化されたデータは暗号化された状態のままで任意の計算が可能となり、イデアル格子を用いGentryによって初めて実現されている。

数学的な背景

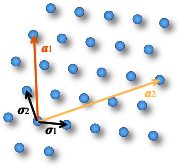
格子 ${\displaystyle L\subset \mathbb {R} ^{n}}$ とは、基底ベクトル${\displaystyle \mathbf {b} _{1},\ldots ,\mathbf {b} _{n}\in \mathbb {R} ^{n}}$の整数線形結合で表現できる全てのベクトルから成る集合である。つまり、${\displaystyle L={\Big \{}\sum a_{i}\mathbf {b} _{i}\ :\ a_{i}\in \mathbb {Z} {\Big \}}}$である。例えば${\displaystyle \mathbb {Z} ^{n}}$ は、普通の直交基底${\displaystyle \mathbb {R} ^{n}}$から生成される格子である。重要なのは、異なる基底が同一の格子を生成しうるということである。たとえば、直交基底 ${\displaystyle (1,0,0)}$、${\displaystyle (0,1,0)}$、${\displaystyle (0,0,1)}$から${\displaystyle \mathbb {Z} ^{3}}$が生成されるが，${\displaystyle (3,1,4)}$、${\displaystyle (1,5,9)}$、${\displaystyle (2,-1,0)}$も同じ格子を生成する別の基底である。

格子を用いた計算量的な問題で最も重要なものは最短ベクトル問題 (SVP，あるいはGapSVP) であり、これは、格子内の非ゼロのベクトルのうち最短のベクトルを求めよ、という問題である。この問題は、近似解 (最短ベクトル長の高々${\displaystyle n}$の多項式倍の長さのベクトル) であっても、効率的に見つけられないと考えられており、さらには量子コンピュータを使ったとしても難しいと考えられている。多くの格子ベース暗号では、SVPを解くのが実際に難しいならば、暗号が破られないことが保障されている。

代表的な格子暗号

暗号方式

• NTRU暗号
• Peikert's Ring - Learning With Errors (Ring-LWE) Key Exchange
• GGH encryption scheme
• CRYSTALS-Kyber

署名方式

• NTRU署名
• Guneysu, Lyubashevsky, Popplemanによる Ring-LWE署名
• GGH signature scheme
• CRYSTALS-Dilithium

ハッシュ関数

• SWIFFT
• LASH (Lattice Based Hash Function)

完全準同型暗号

• Gentryが最初に提案した完全準同型暗号方式
• BrakerskiとVaikuntanathanによる方式

安全性

格子暗号は、耐量子公開鍵暗号の主力候補である。現在の主な公開鍵暗号方式は、素因数分解問題 (あるいはRSA問題) と離散対数問題 (あるいはDiffie-Hellman問題) の困難性に基づく方式である。しかし、素因数分解も離散対数問題も、量子コンピュータを用いると多項式時間で解けることが知られている。また、素因数分解アルゴリズムから離散対数を求めるアルゴリズムが作られたり、逆に離散対数のアルゴリズムが素因数分解に利用される傾向がある。つまり、これらのどちらかを効率的に解く方法が (量子コンピュータ以外の方法で) 見つかった時には、他方も解けてしまう恐れがある。この事実が、格子問題のような、素因数分解と離散対数問題以外の困難性仮定に基づく暗号方式を研究する動機となっている。

多くの格子ベース暗号は、ある格子問題の最悪時の困難性を仮定して、安全性が示されている。つまり、もしその暗号方式を無視できない確率で破る効率的なアルゴリズムが存在したとすれば、格子問題にどんな入力が与えられたとしても効率的に解いてしまうようなアルゴリズムが作れる。これに対して，例えば素因数分解問題に基づく暗号方式の場合は、平均時の困難性を仮定して安全性が示されている。したがって、最悪の入力の素因数分解が困難であったとしても、平均的な入力の素因数分解が簡単である場合には、暗号が破られてしまうかもしれない。とはいえ、効率が良く実用的な格子暗号 (NTRUに基づく方式や、よりaggressiveなパラメータを用いたLWEに基づく方式など) では、最悪ケースの困難性に基づく結果は知られていない。いくつかの方式では、最悪時の困難性に対する安全性は全く知られていないか、structured lattices によるものだけが知られている。

機能

暗号プリミティブによっては、今のところ格子 (やそれに密接に関係したもの) に基づいた方式しか知られていないというものも多い。例えば、完全準同型暗号や識別不可能性を持つ難読化 cryptographic multilinear maps、関数暗号などである。

脚注

参考文献

• Oded Goldreich, Shafi Goldwasser, and Shai Halevi. "Public-key cryptosystems from lattice reduction problems". In CRYPTO ’97: Proceedings of the 17th Annual International Cryptology Conference on Advances in Cryptology, pages 112-131, London, UK, 1997. Springer-Verlag.
• Phong Q. Nguyen. "Cryptanalysis of the Goldreich-Goldwasser-Halevi cryptosystem from crypto ’97". In CRYPTO ’99: Proceedings of the 19th Annual International Cryptology Conference on Advances in Cryptology, pages 288-304, London, UK, 1999. Springer-Verlag.
• Oded Regev. Lattice-based cryptography. In Advances in cryptology (CRYPTO), pages 131-141, 2006.