相互相関関数

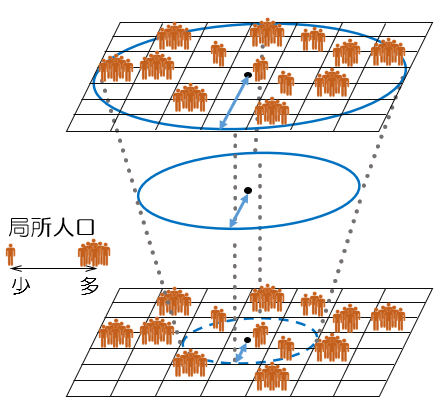
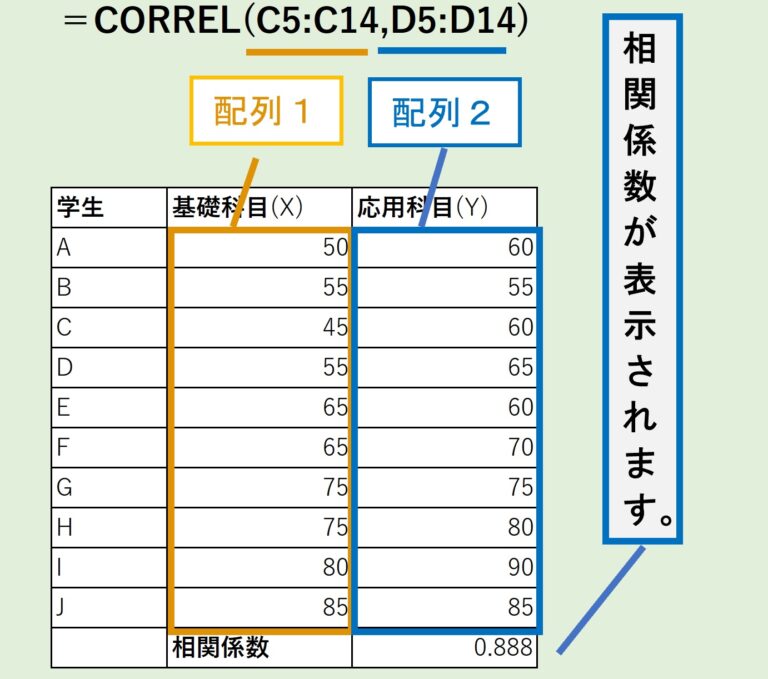
相互相関関数（そうごそうかんかんすう、英: cross-correlation function）は、ふたつの信号、配列（ベクトル）の類似性を確認するために使われる。関数の配列の結果がすべて1であれば相関があり、すべてゼロであれば無相関であり、すべて −1 であれば負の相関がある。しばしば、相関と略されることがあり、相関係数と似ているために混同することがある。

定義

連続

連続関数 ${\displaystyle f}$ と ${\displaystyle g}$ において相互相関関数は以下のように定義される。

${\displaystyle (f\star g)(\tau )\ \triangleq \int _{-\infty }^{\infty }{\overline {f(t)}}g(t \tau )\,dt}$

これは以下と同値である。

${\displaystyle (f\star g)(\tau )\ \triangleq \int _{-\infty }^{\infty }{\overline {f(t-\tau )}}g(t)\,dt}$

${\displaystyle {\overline {f(t)}}}$ は ${\displaystyle f(t)}$ の複素共役で、${\displaystyle \tau }$ はラグ（lag）と呼ばれる。

離散

離散関数の場合は以下のように定義される。

${\displaystyle (f\star g)[n]\ \triangleq \sum _{m=-\infty }^{\infty }{\overline {f[m]}}g[m n]}$

これは以下と同値である。

${\displaystyle (f\star g)[n]\ \triangleq \sum _{m=-\infty }^{\infty }{\overline {f[m-n]}}g[m]}$

畳み込みとの関係性

二つの信号を畳み込む畳み込みの式

${\displaystyle (f*g)(m)=\sum _{n}{f(n)\,g(m-n)}}$

のうち片方の関数の信号配列の順序をフリップ(逆順に)して畳み込むと、相互相関関数を求めることができる。

自己相関関数

二つの信号が、全く同じ場合、自己相関関数と呼び、関数の周期性を調べるのに用いられる。自己相関関数の値がすべて1のときには、その離散関数の波形の周期性はその関数を表す配列と同じであることがわかる。

参照

関連項目

• 畳み込み (convolution)
• インパルス応答 - 伝達関数
• フーリエ変換 - ラプラス変換
• 基本解
• 超関数
• 相関係数
• 自己共分散
• 相互相関関数 (場の量子論)

外部リンク

• 相互相関解析 - 脳科学辞典